Contr?le exact des limites des ¨¦quations d'ondes semi-lin¨¦aires 1D par une approche constructive

L¡¯¨¦quation des ondes mod¨¦lise des ph¨¦nom¨¨nes acoustiques et/ou vibratoires. Pour toute position \(y_0\) et vitesse \(y_1\) initiale, on cherche ¨¤ montrer l¡¯existence d¡¯un contr?le fronti¨¨re \(v\) tel que \(y(1,t)=v(t)\) agissant a l¡¯une des extr¨¦mit¨¦s de l¡¯intervalle \((0,1)\) de fa?on ¨¤ ce que la solution \(y\) atteigne un ¨¦tat cible prescrit \((z_0,z_1)\) ¨¤ l¡¯instant \(T\)

L¡¯existence de tels contr?les est connue depuis un r¨¦sultat de Zuazua en 1993, supposant que la nonlinearit¨¦ \(f\) est localement lipschitz, continue et v¨¦rifie la condition de croissance a l¡¯infini
\[\limsup_{\vert r\vert\to \infty} \vert f(r)\vert /(\vert r\vert \ln^{2}\vert r\vert)\leq \beta\] pour un r¨¦el \(\beta\) positif suffisamment petit.

La preuve non constructive est bas¨¦e sur une lin¨¦arisation de l¡¯¨¦quation et l¡¯application d'un th¨¦or¨¨me de point fixe de Schauder.  

Le travail publi¨¦ en 2023 dans le cadre du post-doctorat du chercheur de nationalit¨¦ indienne Kuntal Bhandari financ¨¦ par l¡¯I-site apportent deux contributions nouvelles: d¡¯une part, il propose une preuve simplifi¨¦e du r¨¦sultat pr¨¦c¨¦dent tout en relaxant le caract¨¨re Lipschitz de la fonction \(f\): cette preuve s¡¯appuie sur un op¨¦rateur de fixe diff¨¦rent ou toute la non lin¨¦arit¨¦ est consid¨¦r¨¦e comme un second membre de l¡®¨¦quation.  D¡¯autre part, en supposant une hypoth¨¨se de croissance ¨¤ l¡¯infini sur la d¨¦riv¨¦e de \(f\) de la forme 
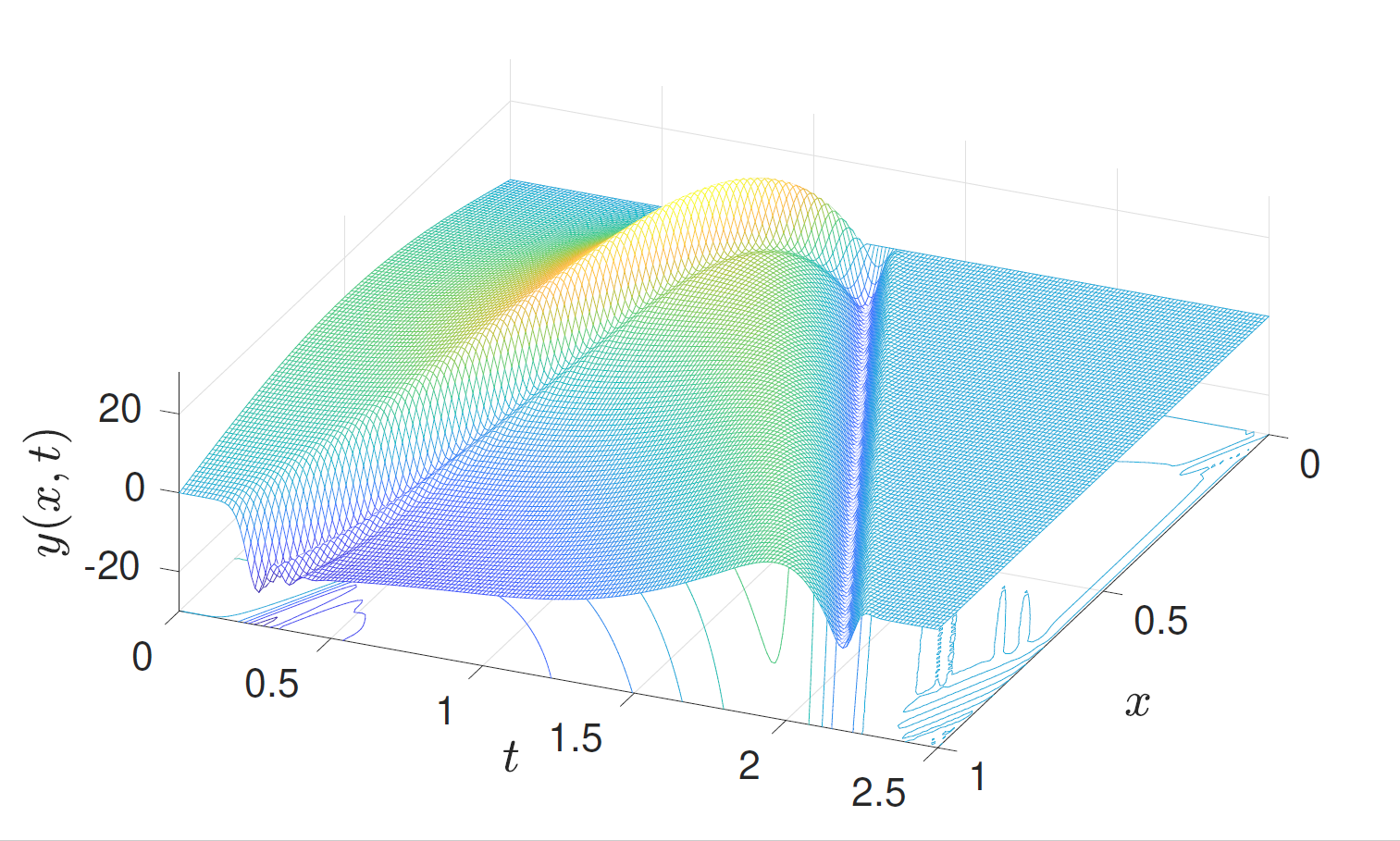
\[\limsup_{\vert r\vert\to \infty} \vert f^\prime(r)\vert/\ln^{3/2}\vert r\vert\leq \beta\] pour un r¨¦el \(\beta\) positif suffisamment petit, on montre que l¡¯op¨¦rateur de point fixe est contractant menant ¨¤ une m¨¦thode d¡¯approximation de contr?les pour l¡¯¨¦quation non lin¨¦arit¨¦ initiale, bas¨¦e sur les it¨¦r¨¦s de Picard de l¡¯op¨¦rateur. La figure repr¨¦sente la solution contr?l¨¦e sur le domaine \((0,1)\times (0,T)\) avec \(T=2.5\), une non lin¨¦arit¨¦ \(f(r)=-3r ln^{3/2}(1+\vert r\vert)\), un ¨¦tat initial \((y_0,y_1)=(10 \sin(\pi x),0)\) et un ¨¦tat cible \((z_0,z_1)=(0,0)\).  L¡¯extension de ces r¨¦sultats en toute dimension d'espace fait l¡¯objet de la th¨¨se de l¡¯¨¦tudiante Sue Claret, d¨¦marr¨¦e en octobre 2022 au LMBP. 

D'apr¨¨s la publication de Bhandari, Kuntal; Lemoine, J¨¦r?me; M¨¹nch, Arnaud, Exact boundary controllability of 1D semilinear wave equations through a constructive approach. Math. Control Signals Systems 35 (2023), no. 1, 77¨C123.